- Home
- About Us
- Chapters
- Study Design and Organizational Structure
- Study Management
- Tenders, Bids, and Contracts
- Sample Design
- Questionnaire Design
- Instrument Technical Design
- Translation
- Adaptation
- Pretesting
- Interviewer Recruitment, Selection, and Training
- Data Collection
- Paradata and Other Auxiliary Data
- Data Harmonization
- Data Processing and Statistical Adjustment
- Data Dissemination
- Statistical Analysis
- Survey Quality
- Ethical Considerations
- Resources
- How to Cite
- Help


Appendix E (Assumptions of Missing Data)
There are there mechanisms for missing data [zotpressInText item="{2265844:M8ZJBZXV}"]. The difference between the three mechanisms depends on the relationship of the variable of interest to the missing observations and the variables available to explain the missingness.
- Missing completely at random (MCAR):
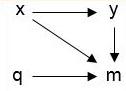
- This missing data mechanism assumes the underlying process causing missing data are uncorrelated with any of the variables in the dataset. In other words, the probability of an observation for variable [latex]y[/latex] being missing does not depend on measurements ([latex]x[/latex] or [latex]y[/latex] in the diagram below) in the dataset itself. An example of MCAR data is missing data due to an instrument malfunction. If MCAR holds, listwise deletion (i.e., an entire record is excluded from analysis if any one value is missing) can be employed, because the available cases constitute a random subsample. Therefore, under MCAR, valid inferences to the target population can be made when analyzing only those units with complete data. If there are variables in the dataset ([latex]x[/latex], [latex]y[/latex]) that help predict the missing values, the assumption does not hold. MCAR rarely holds, and, thus, listwise deletion will seldom be appropriate.
- The concept of MCAR is illustrated below where [latex]y[/latex] is the variable of interest with missing values, [latex]x[/latex] is a predictor of [latex]y[/latex], [latex]m[/latex] is the process causing missingness, and [latex]q[/latex] is a variable not in the dataset.
- Missing at random (MAR):
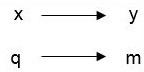
- MAR is a weaker assumption about missingness than MCAR. In MAR, the process causing missing values can be explained by observed, non-missing data ([latex]x[/latex] in the diagram below) other than the variable of interest ([latex]y[/latex]). The probability of data missing on variable [latex]y[/latex] is not related to the value of [latex]y[/latex], controlling for other variables. For data that are MCAR or MAR, the missing data mechanism is deemed ignorable. Note that the missing data mechanism is what is ignorable, not the missing data themselves. For data that are MAR, imputation will reduce bias.
- The concept of MAR is illustrated below where [latex]y[/latex] is the variable of interest with missing values and [latex]x[/latex] is a predictor of [latex]y[/latex] and also can predict the mechanism for missing values, [latex]m[/latex]. [latex]q[/latex] is auxiliary to the dataset and also predicts [latex]m[/latex].
- Missing not at random (MNAR):
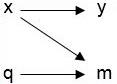
- For data that are MNAR, even after controlling for other observed variables in the dataset ([latex]x[/latex] in the diagram below), the reason for a variable [latex]y[/latex] having missing observations still depends on the unseen observations of [latex]y[/latex] itself. One example of data that could be MNAR is reported income. Individuals with either high or low incomes can be reluctant to report how much they earn. If this is true, the probability of obtaining a measure of a person’s income will depend upon the amount the person earns. Nonignorable nonresponse creates data that are MNAR and, hence, a method of imputation that accounts for this is necessary.
- In the diagram below, [latex]y[/latex] is the variable of interest with missing values, [latex]x[/latex] is a predictor of [latex]y[/latex] in the dataset, and [latex]q[/latex] is unobserved auxiliary data. The three variables [latex]y[/latex], [latex]x[/latex], and [latex]q[/latex] all predict [latex]m[/latex], the mechanism of missing values.